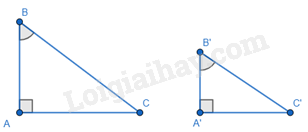
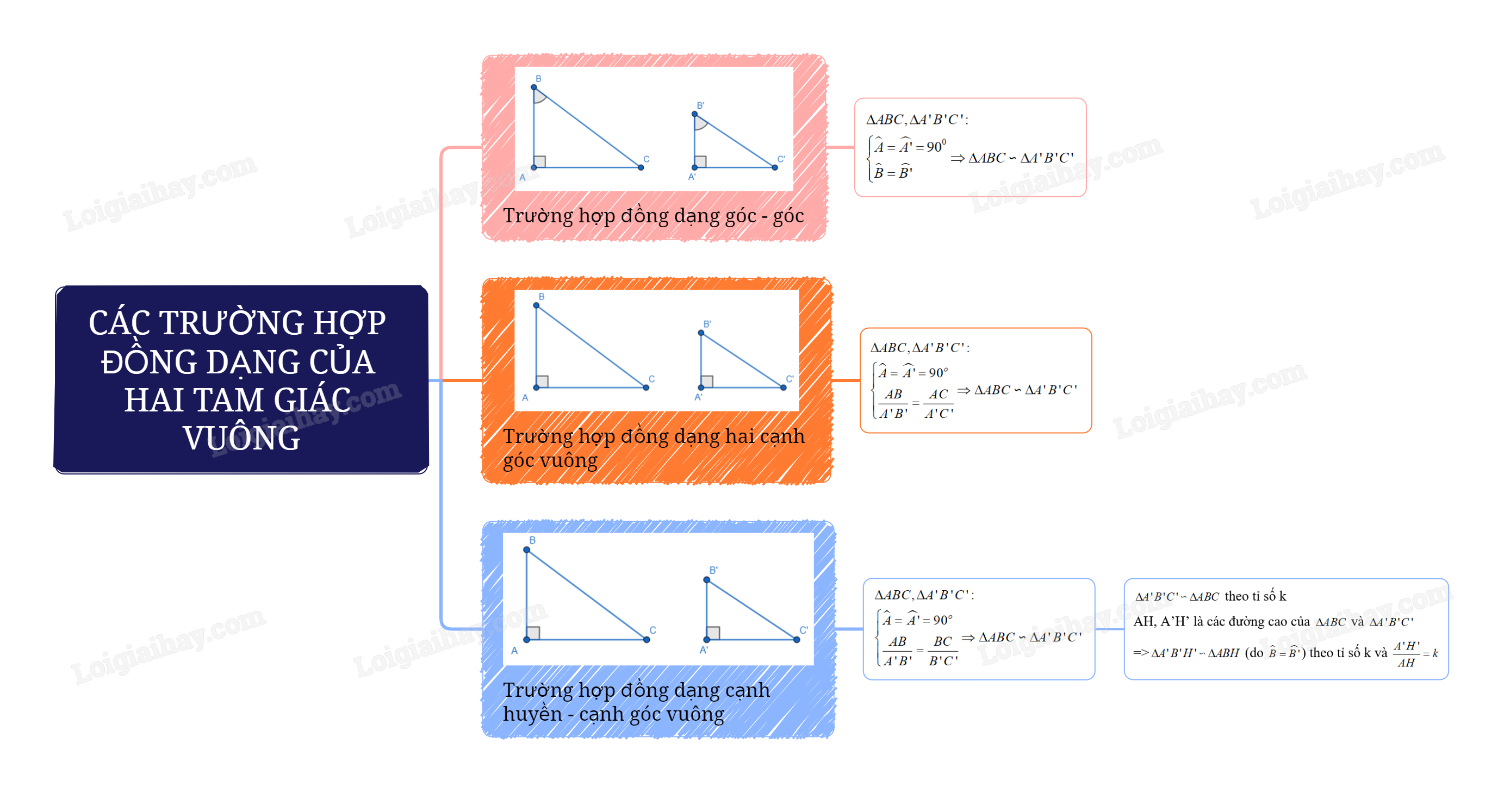
Lý thuyết Các trường hợp đồng dạng của hai tam giác vuông SGK Toán 8 - Kết nối tri thức

1. Trường hợp góc – góc: 

Nếu một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia thì hai tam giác vuông đồng dạng với nhau.

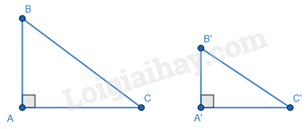
\(\begin{array}{l}\Delta ABC,\Delta A'B'C':\\\left\{ \begin{array}{l}\widehat A = \widehat {A'} = {90^0}\\\widehat B = \widehat {B'}\end{array} \right. \Rightarrow \Delta ABC \backsim \Delta A'B'C'\end{array}\)

2. Trường hợp hai cạnh góc vuông:

Nếu hai cạnh góc vuông của tam giác vuông này tỉ lệ với hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

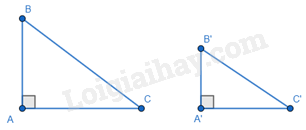
\(\begin{array}{l}\Delta ABC,\Delta A'B'C':\\\left\{ \begin{array}{l}\widehat A = \widehat {A'} = {90^o}\\\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}}\end{array} \right. \Rightarrow \Delta ABC \backsim \Delta A'B'C'\end{array}\)

3. Trường hợp cạnh huyền – cạnh góc vuông:

Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng với nhau.

\(\begin{array}{l}\Delta ABC,\Delta A'B'C':\\\left\{ \begin{array}{l}\widehat A = \widehat {A'} = {90^o}\\\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\end{array} \right. \Rightarrow \Delta ABC \backsim \Delta A'B'C'\end{array}\)

Nhận xét: Nếu \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số k và AH, A’H’ lần lượt là các đường cao của \(\Delta ABC\) và \(\Delta A'B'C'\) thì \(\Delta A'B'H' \backsim \Delta ABH\) (do \(\widehat B = \widehat {B'}\)) theo tỉ số k và \(\frac{{A'H'}}{{AH}} = k\).