Cho hàm số \(f\left( x \right) = \sqrt {x + 1} \). Tính đạo hàm của hàm số tại điểm \({x_0} = 1\)

Khi tính đạo hàm của hàm số \(f\left( x \right) = {x^2} + 5x - 3\) tại điểm \({x_0} = 2\), một học sinh đã tính theo các bước sau:

Bước 1: \(f\left( x \right) - f\left( 2 \right) = f\left( x \right) - 11\)

Bước 2: \(\dfrac{{f\left( x \right) - f\left( 2 \right)}}{{x - 2}} = \dfrac{{{x^2} + 5x - 3 - 11}}{{x - 2}} = \dfrac{{\left( {x - 2} \right)\left( {x + 7} \right)}}{{x - 2}} = x + 7\)

Bước 3: \(\mathop {\lim }\limits_{x \to 2} \dfrac{{f\left( x \right) - f\left( 2 \right)}}{{x - 2}} = \mathop {\lim }\limits_{x \to 2} \left( {x + 7} \right) = 9 \Rightarrow f'\left( 2 \right) = 9\)

Tính toán trên nếu sai thì sai ở bước nào?

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}3 - \sqrt {4 - x} \,\,\,khi\,\,x \ne 0\\1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\) . Khi đó \(f'\left( 0 \right)\) là kết quả nào sau đây?

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\sqrt x \,\,\,khi\,\,x > 1\\{x^2}\,\,\,\,\,khi\,\,x \le 1\end{array} \right.\). Tính \(f'\left( 1 \right)\) ?

Tính tỷ số \(\dfrac{{\Delta y}}{{\Delta x}}\) của hàm số \(y = 2{x^3}\) theo \(x\) và \(\Delta x.\)

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}2x + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 1\\\dfrac{{{x^3} + 2{x^2} - 7x + 4}}{{x - 1}}\,\,khi\,\,x < 1\end{array} \right.\). Giá trị của \(f'\left( 1 \right)\) bằng:

Cho hàm số \(y = f\left( x \right)\) xác định: \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {{x^2} + 1}  - 1}}{x}\,\,khi\,\,x \ne 0\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\). Giá trị của \(f'\left( 0 \right)\) bằng:

Xét hai hàm số: \(\left( I \right):f\left( x \right) = \left| x \right|x,\,\,\left( {II} \right):g\left( x \right) = \sqrt x \) . Hàm số có đạo hàm tại $x = 0$ là:

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt[3]{{4{x^2} + 8}} - \sqrt {8{x^2} + 4} }}{x}\,\,\,khi\,x \ne 0\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,x = 0\end{array} \right.\). Giá trị của \(f'\left( 0 \right)\) bằng:

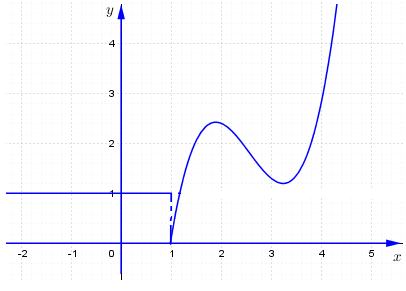
Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ. Mệnh đề nào sau đây sai?

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^3} - 4{x^2} + 3x}}{{{x^2} - 3x + 2}}\,\,\,khi\,\,x \ne 1\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\). Giá trị của \(f'\left( 1 \right)\) bằng:

Cho hàm số \(f\left( x \right) = \dfrac{{{x^2} + \left| {x + 1} \right|}}{x}\). Tính đạo hàm của hàm số tại \({x_0} =  - 1\).

Xét hai câu sau:

(1) Hàm số \(y = \dfrac{{\left| x \right|}}{{x + 1}}\) liên tục tại $x = 0.$

(2) Hàm số \(y = \dfrac{{\left| x \right|}}{{x + 1}}\) có đạo hàm tại $x = 0.$

Trong 2 câu trên:

Tìm $a$ để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^2} - 1}}{{x - 1}}\,\,khi\,\,x \ne 1\\a\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 1\end{array} \right.\) có đạo hàm tại $x = 1.$

Tìm $a, b$ để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{{x^2} + 1}}{{x + 1}}\,\,khi\,\,x \ge 0\\ax + b\,\,khi\,\,x < 0\end{array} \right.\)  có đạo hàm tại điểm $x = 0.$

Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}a{x^2} + bx\,\,khi\,\,x \ge 1\\2x - 1\,\,\,\,\,\,\,khi\,\,x < 1\end{array} \right.\). Tìm $a, b$ để hàm số có đạo hàm tại $x = 1.$

Với hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x\sin \dfrac{\pi }{x}\,\,khi\,\,x \ne 0\\0\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\) . Để tìm đạo hàm \(f'\left( 0 \right)\) một học sinh lập luận qua các bước sau:

Bước 1: \(\left| {f\left( x \right)} \right| = \left| x \right|\left| {\sin \dfrac{\pi }{x}} \right| \le \left| x \right|\)

Bước 2: Khi \(x \to 0\) thì \(\left| x \right| \to 0\)  nên \(\left| {f\left( x \right)} \right| \to 0 \Rightarrow f\left( x \right) \to 0\)

Bước 3: Do \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right) = 0\)  nên hàm số liên tục tại $x = 0.$

Bước 4: Từ $f(x)$ liên tục tại \(x = 0 \Rightarrow f\left( x \right)\) có đạo hàm tại $x = 0.$

Lập luận trên nếu sai thì bắt đầu từ bước nào?

Cho hàm số \(f\left( x \right) = x\left( {x - 1} \right)\left( {x - 2} \right)...\left( {x - 1000} \right)\). Tính \(f'\left( 0 \right)\) ?

Tìm $a, b$ để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}a{x^2} + bx + 1\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 0\\a\sin x + b\cos x\,\,\,\,khi\,\,x < 0\end{array} \right.\)  có đạo hàm tại điểm \({x_0} = 0\).