Cho các đoạn thẳng \(AB = 8{\rm{ cm, }}CD = 6{\rm{ cm, }}MN = 12{\rm{ cm, }}PQ = x{\rm{ cm}}\) . Tìm \(x\) để \(AB\) và \(CD\) tỉ lệ với \(MN\) và \(PQ\) .
- A. 7 cm
- B. 8 cm
- C. 9 cm
- D. 10 cm
Dựa vào định nghĩa hai đoạn thẳng tỉ lệ: Hai đoạn thẳng \(AB\) và \(CD\) gọi là tỉ lệ với hai đoạn thẳng \(A'B'\) và \(C'D'\) nếu có tỉ lệ thức: \(\frac{{AB}}{{CD}} = \frac{{A'B'}}{{C'D'}}\) hay \(\frac{{AB}}{{A'B'}} = \frac{{CD}}{{C'D'}}\) .
\(\begin{array}{l}\frac{{AB}}{{CD}} = \frac{8}{6} = \frac{4}{3}\\\frac{{MN}}{{PQ}} = \frac{{12}}{x}\\\frac{{AB}}{{CD}} = \frac{{MN}}{{PQ}} \Leftrightarrow \frac{4}{3} = \frac{{12}}{x} \Leftrightarrow x = \frac{{12.3}}{4} = 9\end{array}\)
Đáp án : C

Các bài tập cùng chuyên đề
Cho \(AB = 6\,{\rm{cm, }}AC = 18\,{\rm{cm}}\) , tỉ số hai đoạn thẳng \(AB\) và \(AC\) là:
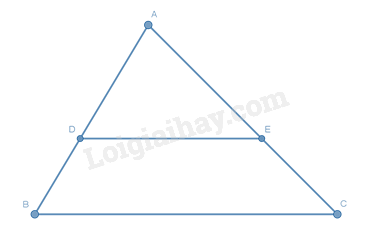
Cho tam giác \(ABC\) như hình vẽ dưới đây. Hãy chọn khẳng định sai:
Cho các đoạn thẳng \(AB = 6\,{\rm{cm,}}\,CD = 4\,{\rm{cm,}}\,PQ = 8\,{\rm{cm,}}\,EF = 10\,{\rm{cm,}}\) \(MN = 25{\rm{ mm, }}RS = 15\,{\rm{mm}}\) . Hãy chọn các phát biểu đúng trong các phát biểu sau:
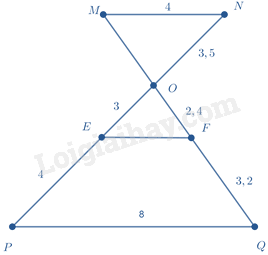
Cho hình vẽ sau. Có bao nhiêu cặp đường thẳng song song?
Cho điểm \(C\) thuộc đoạn thẳng \(AB\) thỏa mãn \(\frac{{AC}}{{BC}} = \frac{3}{5}\) . Tính tỉ số \(\frac{{AC}}{{AB}}\) .
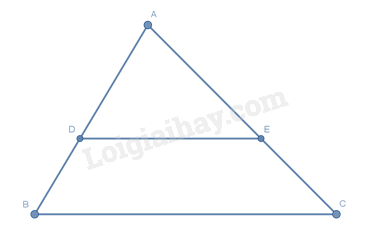
Cho hình vẽ sau, biết \(DE // BC\) . \(AD = 8,\,DB = 6,\,CE = 9\) . Độ dài \(AC\) bằng?
Cho hình vẽ dưới dây. Tính \(OM\) .
Cho tam giác \(ABC\) có \(AB = 12{\rm{ cm}}\) , điểm \(D\) thuộc cạnh \(AB\) sao cho \(AD = 8{\rm{ cm}}\) . Kẻ \(DE\) song song với \(BC\,\left( {E \in AC} \right)\) , kẻ \(EF\) song song với \(CD\,\left( {F \in AB} \right)\) . Tính độ dài \(AF\) .
Cho tứ giác \(ABCD\) có \(O\) là giao điểm của hai đường chéo. Đường thẳng qua \(A\) và song song với \(BC\) cắt \(BD\) ở \(E\) . Đường thẳng qua \(B\) song song với \(AD\) cắt \(AC\) ở \(F\) . Chọn kết luận sai?
Cho tứ giác\(ABCD\) . Lấy điểm\(E\) bất kì thuộc\(BD\) . Qua\(E\) kẻ\(EF\) song song với\(AD\left( {F \in AB} \right)\) , kẻ\(EG\) song song với\(DC\,\left( {G \in BC} \right)\) . Chọn khẳng định sai:
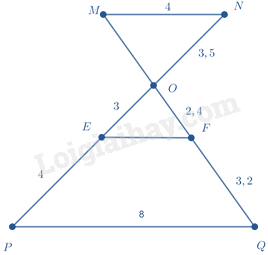
Cho điểm\(M\) thuộc đoạn thẳng\(AB\) sao cho\(MA = 2MB\) . Vẽ về một phía của\(AB\) các tam giác đều\(AMC\) và\(MBD\) . Gọi\(E\) là giao điểm của\(AD\) và\(MC\) ,\(F\) là giao điểm của\(BC\) và\(DM\) . Đặt\(MB = a\) . Tính\(ME,MF\) theo\(a\) .
Cho hình thang\(ABCD\left( {AB // CD} \right)\) có diện tích\(48\,{\rm{c}}{{\rm{m}}^2}\) ,\(AB = 4\,{\rm{cm,}}\,CD = 8{\rm{cm}}\) . Gọi\(O\) là giao điểm của hai đường chéo. Tính diện tích tam giác\(COD\)
Cho hình thang\(ABCD\,\left( {AB // CD} \right)\) có\(BC = 18{\rm{ cm,}}\,AD = 12{\rm{ cm}}\) . Điểm\(E\) thuộc cạnh\(AD\) sao cho\(AE = 6{\rm{ cm}}\) . Qua\(E\) kẻ đường thẳng song song với\(CD\) , cắt\(BC\) ở\(F\) . Tính độ dài\(BF\) .
Cho hình thang\(ABCD\,\left( {AB // CD} \right)\) . Một đường thẳng song song với\(AB\) cắt các cạnh bên\(AD,\,BC\) theo thứ tự ở\(E,\,F\) . Đẳng thức nào sau đây đúng?
Cho tam giác\(ABC\) có\(AM\) là trung tuyến và điểm\(E\) thuộc đoạn thẳng\(MC\) . Qua\(E\) kẻ đường thẳng song song với\(AC\) , cắt\(AB\) ở\(D\) và cắt\(AM\) ở\(K\) . Qua\(E\) kẻ đường thẳng song song với\(AB\) , cắt\(AC\) ở\(F\) . Hãy chọn khẳng định sai.
Cho tứ giác\(ABCD\) . Qua\(E \in AD\) kẻ đường thẳng song song với\(DC\) cắt\(AC\) ở\(G\) . Qua\(G\) kẻ đường thẳng song song với\(CB\) cắt\(AB\) tại\(H\) . Qua\(B\) kẻ đường thẳng song song với\(CD\) , cắt đường thẳng\(AC\) tại\(I\) . Qua\(C\) kẻ đường thẳng song song với\(BA\) , cắt\(BD\) tại\(F\) . Khẳng định nào sau đây là sai?
Cho hình thang\(ABCD\left( {AB // CD} \right)\) .\(M\) là trung điểm của\(CD\) . Gọi\(I\) là giao điểm của\(AM\) và\(BD\) ,\(K\) là giao điểm của\(BM\) và\(AC\) . Đường thẳng\(IK\) cắt\(AD,\,BC\) theo thứ tự ở\(E\) và\(F\) . Có bao nhiêu khẳng định đúng trong các khẳng định sau?
(I)\(IK // AB\)
(II)\(EI = IK = KF\)
(III)\(\frac{{DI}}{{BD}} = \frac{{IM}}{{AM}}\)
Cho tam giác \(ABC\) có đường cao \(AH\) . Trên \(AH\) lấy các điểm \(K,\,I\) sao cho \(AK = KI = IH\). Qua \(I,\,K\) lần lượt vẽ các đường thẳng \(EF // BC,\,MN // BC\) \(\left( {E,\,M \in AB;\,F,\,N \in AC} \right)\) . Cho biết diện tích của tam giác \(ABC\) là \(90\,{\rm{c}}{{\rm{m}}^2}\) . Hãy tính diện tích tứ giác \(MNF\) .
Cho đoạn thẳng\(ABC\) , điểm\(I\) nằm trong tam giác. Các tia\(AI,\,BI,CI\) cắt các cạnh\(BC,\,AC,\,AB\) theo thứ tự ở\(D,\,E,\,F\) . Tổng\(\frac{{AF}}{{FB}} + \frac{{AE}}{{EC}}\) bằng tỉ số nào dưới đây?